Fórmulas, funciones y métodos para el análisis estadístico

La media estadística es lo que habitualmente llamamos promedio.

La fórmula para calcular tanto la media poblacional como la media muestral es la misma:

Media es igual al sumatorio de todos los valores de la variable x dividido por el número de observaciones.

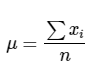
Media poblacional

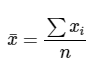
Media muestral

La media estadística puede ser calculada con la función mean() de R.

Por ejemplo, busquemos la media de los valores 4,15,6,28,39 :

values <- c(4,15,6,28,39)

mean(values)

El resultado será 18,4.

Para obtener la media estadística, podemos utilizar el método mean() de la librería NumPy. Por ejemplo, para encontrar la media de los valores 3, 7, 25, 4, 72, 15:

import numpy

values = [3,7,25,4,72,15]

x = numpy.mean(values)

print(x)

Para calcular la media estadística con Excel, aplicamos la siguiente función:

PROMEDIO(número1; [número2]; …)

Por ejemplo:

=PROMEDIO(A2:A6)
Promedio de los números en las celdas A2 a A6.

La mediana estadística de una serie ordenada de datos numéricos es la cifra que queda justo en medio, en el sentido de que la mitad de los datos estarán a su izquierda y la otra mitad, a la derecha.

La fórmula para calcular la mediana estadística es:

Número total de observaciones más 1, dividido por 2.

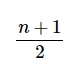
Mediana

Con R, obtenemos la mediana estadística con la función median(). Por ejemplo:

values <- c(13,21,21,40,42,48,55,72)

median(values)

Podemos obtener la mediana estadística usando el método median() de la librería NumPy.

Por ejemplo:

import numpy

values = [8,25,25,38,42,47,79]

x = numpy.median(values)

print(x)

La moda estadística de una variable cuantitativa es el valor que presenta una mayor frecuencia.

En R no existe una función predifinida para obtener la moda estadística, así que podemos emplear una función de usuario. Por ejemplo:

mode <- function(x) {
unique_values <- unique(x)
table <- tabulate(match(x, unique_values))
unique_values[table == max(table)] }

values <- c(4,7,3,8,11,7,10,19,6,9,12,12)

mode(values)

Usando el método multimode() de la librería estadística de Python podemos identificar la moda estadística de una serie de datos:

from statistics import multimode

values = [5,2,26,5,13,81,40,13]

x = multimode(values)

print(x)

La sintaxis de la función moda de Excel, que nos permite identificar la moda estadística en una serie de datos, sería MODA(número1,[número2],…).

Por ejemplo:

=MODA(A2:A7)

Un cuartil de un conjunto ordenado de datos numéricos es cada uno de los tres puntos de corte que dividen el conjunto en cuatro grupos de la misma medida.

• El primer cuartil (Q1) es el dato que separa el 25% inferior del resto del conjunto de datos.
• El segundo cuartil (Q2) corresponde a la media estadística de los datos.
• El tercer cuartil (Q3) es el dato que separa el 75% inferior del resto de datos del conjunto.

La función quantile() de R nos permite encontrar fácilmente los cuartiles de un conjunto de valores numéricos. Por ejemplo:

values <- c(13,21,21,40,42,48,55,72)

quantile(values)

Con el método quantile() de la librería NumPy de Python podemos encontrar los cuartiles de un conjunto de valores. Por ejemplo:

import numpy

values = [13,21,21,40,42,48,55,72]

x = numpy.quantile(values, [0,0.25,0.5,0.75,1])

print(x)

La función CUARTIL de Excel devuelve el cuartil de un conjunto de datos numéricos.

La sintaxis de la función sería la siguiente:

CUARTIL(matriz,cuartil)

Por ejemplo:

=CUARTIL(A2:A9;1) devolvería el valor del primer cuartil de los datos incluidos desde la celda A2 hasta la celda A9 de una hoja de cálculo.

Un percentil es una medida de posición no central que permite, en un conjunto de datos numéricos ordentado de menor a mayor, determinar el valor de la variable por debajo del cual se encuentra un porcentaje dado de observaciones de dichos datos. Los percentiles son los 99 cuantiles que separan el conjunto de datos en 100 partes iguales.

La fórmula para encontrar un determinado percentil sería:

Pi = X (( N + 1) i ) / 100

N representa el número de observaciones o datos del conjunto.

La función quantile() de R permite encontrar un determinado percentil en un conjunto de valores numéricos.

Por ejemplo:

values <- c(9,23,35,40,40,78,92,92,101)

quantile(values, 0.65)

Con esta función obtendríamos el valor del percentil 65º de los datos antes indicados; es decir, 80,8.

Con el método percentile() de la librería NumPy podremos encontrar un percentil de un conjunto de valores numéricos.

Por ejemplo:

import numpy

values = [13,21,21,40,42,48,55,72]

x = numpy.percentile(values, 65)

print(x)

Esto nos devolvería el valor del percentil 65º de los valores indicados; es decir, 45,3.

En Excel, la función PERCENTIL nos sirve para identificar el valor de un determinado percentil en un conjunto de datos.

La sintaxis de la función es como sigue:

PERCENTIL(matriz,k)

Por ejemplo:

=PERCENTILE(E2:E5,0.3)

En este caso obtendríamos el percentil 30 de la lista en las celdas desde E2 hasta E5.

La forma de calcular el rango es restar el valor menor del valor mayor.

Por ejemplo:

89 – 12 = 77

Para calcular el rango estadístico con la ayuda de Excel nos valdremos de la fórmula para identificar el número mayor de una selección de celdas (función MAX) y la fórmula para encontrar el número menor (función MIN) y realizaremos la resta entre ambos números.

Estos son los pasos que deberíamos seguir:

1. Seleccionamos la celda en la que queremos mostrar el resultado del rango.
2. En la barra de fórmulas escribimos =MAX(selección de celdas) – MIN(selección de celdas).
3. Pulsamos Enter.

Rango Excel

Con las funciones de R min() y max() podemos obtener el rango estadístico de una serie de valores numéricos. Por ejemplo:

values <- c(12,27,40,40,48,63,90)

max(values) – min(values)

El rango estadístico se puede obtener mediante el método ptp() de la librería NumPy. Por ejemplo:

import numpy

values = [9,25,40,40,54,55,80]

x = numpy.ptp(values)

print(x)

.

El rango intercuartil es la medida de la diferencia entre el primer cuartil (Q1) y el tercer cuartil (Q3).

En R podemos emplear la función IQR() para conocer el rango intercuartil de un conjunto de valores.

Por ejemplo:

values <- c(23,24,52,67,80,80,93,104)

IQR(values)

En este caso, el resultado será 38,25.

Con el método iqr() de la librería de Python SciPy podremos obtener el rango intercuartil de un conjunto de datos.

Por ejemplo:

from scipy import stats

values = [9,13,13,28,41,41,56,82]

x = stats.iqr(values)

print(x)

El resultado sería 31,75.

Las fórmulas para el cálculo de la desviación estándar de la población estadística o el de la muestra estadística son bastante similares aunque no idénticas.

La desviación estándar poblacional es igual a la raíz cuadrada del sumatorio de la primera potencia de la diferencia entre los valores de las observaciones y la media poblacional y luego dividido por el número de observaciones.

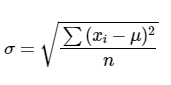
La desviación estándar muestral es igual a la raíz cuadrada del sumatorio de la primera potencia de la diferencia entre los valores de las observaciones y la media muestral y luego dividido por el número de observaciones menos 1.

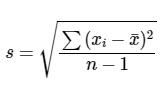
Podemos usar una fórmula de R para encontrar la desviación estándar de un conjunto de valores.

Por ejemplo:

values <- c(7,11,18,22)

sqrt(mean((values-mean(values))^2))

El resultado será 5.85235.

Podemos obtener la desviación estándar usando el método std() de la librería NumPy.

Por ejemplo:

import numpy

values = [7,11,18,22]

x = numpy.std(values)

print(x)

El resultado dará 5.852349955359813.

Para calcular la puntuación Z calculamos el valor estandarizado menos la media poblacional y el resultado de esta sustracción lo dividimos por la desviación estándar:

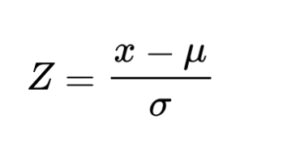
x es el valor estandarizado.

μ (mu) es la media poblacional.

σ (sigma) es la desviación estándar.

En R usaremos la función qnorm() para encontrar el valor Z de, por ejemplo, un valor p de 0,9:

qnorm(0.9)

Podemos encontrar el valor Z de un valor p usando la función norm.ppf() de la librería Scipy Stats para Python. Por ejemplo, si tenemos un valor p de 0.9:

import scipy.stats as stats
print(stats.norm.ppf(0.9))

Para una prueba de cola inferior, el valor p se especifica mediante:

valor p = P(TS ts | H 0 es verdadera) = cdf(ts)

Para una prueba de cola superior se especifica mediante:

valor p = P(TS ts | H 0 es verdadera) = 1 – cdf(ts)

En lenguaje R utilizamos la función pnorm() para conocer el valor p de una puntuación Z.

Por ejemplo, si queremos saber cuánta probabilidad hay de que obtengamos un valor que esté a menos de 3 desviaciones estándares de la media, escribiríamos:

pnorm(3)

El resultado será 0.9986501 o 99.87%.

Podemos recurrir a la función norm.cdf() de la librería Scipy Stats para Python para calcular el valor p de un valor Z.

Por ejemplo, si queremos saber qué probabilidad hay de tener un valor que se encuentre a menos de 3 desviaciones estándares de la media, la sintaxis sería la siguiente:

import scipy.stats as stats
print(stats.norm.cdf(3))

El resultado será 0.9986501019683699 o 99,87%.